n-vector explained

This page gives a brief introduction to n-vector.

What is n-vector?

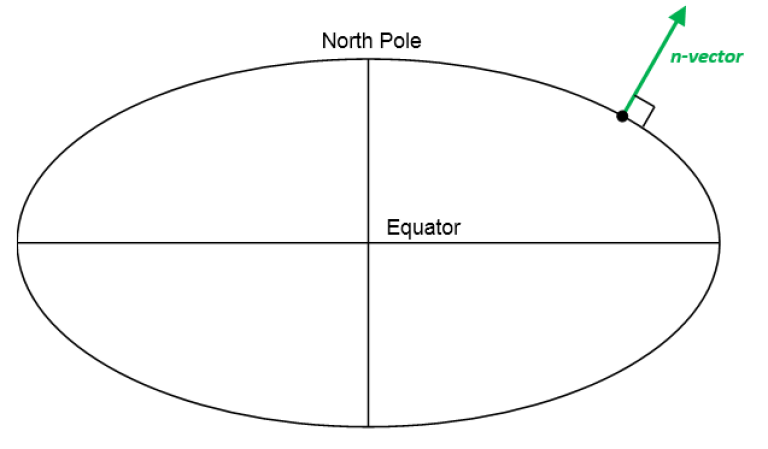
n-vector is just the 3D normal vector to the Earth ellipsoid (or sphere, if spherical Earth model is used). It can replace latitude and longitude (and other alternatives) to represent horizontal position, giving several advantages. This page gives a brief introduction, see Gade (2010) for a more detailed explanation.

 
earthellipsoid3.png
The n-vector is the normal vector to the Earth model (reference ellipsoid).

 

Why is n-vector needed?

Performing global position calculations often involves one or more of the following concerns:
1. Complex implementations (many, and often complex lines of program code needed)
2. Approximations, e.g.
     a. distortion in map projections
     b. assuming spherical Earth when ellipsoidal should be used
     Errors often increase with increasing distances
3. Equation/code not valid/accurate for all Earth positions, e.g.
     a. Latitude/longitude:
         i. Singularities at Poles 
         ii. Discontinuity at International Date Line (±180° meridian)
     b. Map projections: usually valid for a limited area, e.g. UTM
4. Iterations (need to iterate to achieve needed accuracy)

By using n-vector and the solutions provided here, these concerns can be avoided for a majority of position calculations.

Read more

Abstract futuristic technology background with fractal horizon

The n-vector page

The-n-vector page with ten common geographical position calculations

What can go wrong if using latitude and longitude?

Even the simple discontinuity of longitude at the International Date Line (±180° meridian) can give serious consequences if not handled correctly in all the code. An example illustrating this was the computer crash experienced by 12 fighter aircrafts (F-22 Raptors) when they crossed this meridian in 2007.

The discontinuity can be quite easily handled by adding specific code, while the singularities at the Poles are much more challenging to deal with. Examples of how the singularities can affect calculations with latitude and longitude are found in Section 6 in Gade (2010).

F22 Raptors fly over the Pacific Ocean
The discontinuity of longitude caused serious problems for the F-22 Raptors when the longitude instantly changed from -180° to +180° (when crossing the International Date Line). Photo: U.S. Air Force/Master Sgt. Kevin J. Gruenwald / Wikimedia Commons public domain

n-vector

As discussed above, using latitude and longitude in calculations may lead to several problems due to the singularities at the Poles and complex behavior near the Poles, and due to the discontinuity at the Date Line (±180° meridian).

Instead of latitude and longitude, we represent position with an “n-vector”, which is the normal vector to the Earth model (the same reference ellipsoid that is used for latitude and longitude). When using n-vector, all Earth-positions are treated equally, and there is no need to worry about singularities or discontinuities. An additional benefit with using n-vector is that many position calculations can be solved with simple vector algebra (e.g. dot product and cross product).

In documents n-vector is written 
n E MathType@MTEF@5@5@+= feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiFv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabmqaamaabaabaaGcbaGaaCizamaaCa aaleqabaGaamyraaaaaaa@380A@
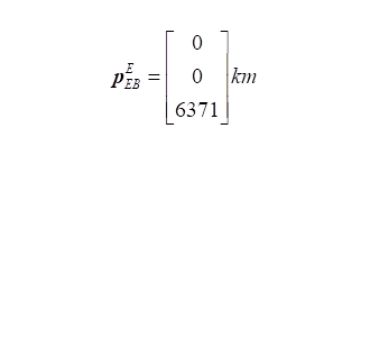
, while in program code we use n_E. E denotes an Earth-fixed coordinate frame, and it indicates that the three components of n-vector are along the three axes of E. More details about the notation used are found here. The position of the North Pole given as n-vector is
nE=001
(assuming the coordinate frame E has its z-axis pointing to the North Pole). For all the details about n-vector, see the reference Gade (2010). 
 

Converting between n-vector and lat/long

Calculating n-vector from latitude/longitude is done using
 
nE=cos(lat)cos(long)cos(lat)sin(long)sin(lat)MathType@MTEF@5@5@+=feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabmqaamaabaabaaGcbaGaaCOBamaaCaaaleqabaGaamyraaaakiabg2da9maadmaabaqbaeqabmqaaaqaaiGacogacaGGVbGaai4CaiaacIcacaWGSbGaamyyaiaadshacaGGPaGaci4yaiaac+gacaGGZbGaaiikaiaadYgacaWGVbGaamOBaiaadEgacaGGPaaabaGaci4yaiaac+gacaGGZbGaaiikaiaadYgacaWGHbGaamiDaiaacMcaciGGZbGaaiyAaiaac6gacaGGOaGaamiBaiaad+gacaWGUbGaam4zaiaacMcaaeaaciGGZbGaaiyAaiaac6gacaGGOaGaamiBaiaadggacaWG0bGaaiykaaaaaiaawUfacaGLDbaaaaa@5FD3@
 
This can be seen from the geometry and the axes of E. The relation is true both for ellipsoidal or spherical Earth model.
 
To find latitude from n-vector we have
 
lat=asin(nzE)=atan2nzE,nxE2+nyE2MathType@MTEF@5@5@+=feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabmqaamaabaabaaGcbaGaamiBaiaadggacaWG0bGaeyypa0JaciyyaiaacohacaGGPbGaaiOBaiaacIcacaWGUbWaa0baaSqaaiaadQhaaeaacaWGfbaaaOGaaiykaiabg2da9iaabggacaqG0bGaaeyyaiaab6gacaqGYaWaaeWaaeaacaWGUbWaa0baaSqaaiaadQhaaeaacaWGfbaaaOGaaiilamaakaaabaWaaeWaaeaacaWGUbWaa0baaSqaaiaadIhaaeaacaWGfbaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaey4kaSYaaeWaaeaacaWGUbWaa0baaSqaaiaadMhaaeaacaWGfbaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaqabaaakiaawIcacaGLPaaaaaa@5839@
 
where the x, y and z subscripts indicate elements 1, 2 and 3 of the n-vector. Note that the atan2-variant has better numerical properties, and is thus recommended for implementation.
 
Longitude is found from
 
long=atan2nyE,nxEMathType@MTEF@5@5@+=feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabmqaamaabaabaaGcbaGaamiBaiaad+gacaWGUbGaam4zaiabg2da9iaabggacaqG0bGaaeyyaiaab6gacaqGYaWaaeWaaeaacaWGUbWaa0baaSqaaiaadMhaaeaacaWGfbaaaOGaaiilaiaad6gadaqhaaWcbaGaamiEaaqaaiaadweaaaaakiaawIcacaGLPaaaaaa@4741@
 
In the downloadable code, two functions lat_long2n_E and n_E2lat_long are used for these conversions.
 

Many position calculations can be solved with only two functions

It turns out that very often, the problem to be solved is one of these:

  1. A and B => delta: Given two positions, A and B (e.g. as latitudes/longitudes/heights), find the (delta) vector from A to B in meters. See also Example 1. 
  2. A and delta => B: Given position A (e.g. as lat/long/height) and a vector in meters from A to B, find position B. See also Example 2.
Two functions performing these calculations are available for download, using n-vectors for position A and B as input/output. The n-vectors for position A and B are written 
nEAE
and 
nEBE
, while in program code we use n_EA_E and n_EB_E. The (delta) position vector from A to B is written 
pABE
(p_AB_E). More information about the notation is found here. 
 
Based on the above variable names, the two above functions are called:
  1. n_EA_E_and_n_EB_E2p_AB_E
  2. n_EA_E_and_p_AB_E2n_EB_E

By default, these functions use the WGS-84 ellipsoid, but any custom ellipsoid (or sphere) may be specified.

n-vector
Navigation

Useful pages

Vector symbols explained

Here you will find the mathematical notation used for the n-vector page.

n-vector downloads

The functions are available in Matlab, C#, C++, Python, JavaScript, and other languages.

The n-vector page

This web page contains solutions to ten common geographical position calculations