n-vektor – eksakte posisjonsberegninger på elliptisk jord

Posisjonsberegninger er sentralt for en rekke av Forsvarets anvendelser, og dermed inngår dette i mange FFI-prosjekter. Noen eksempler på anvendelser er overvåkning, navigasjon, kartvisninger, ruteplanlegging og posisjonering av bilder fra radar, sonar eller kamera. Eksempler på posisjonsberegninger kan være å finne en avstand, et midtpunkt, en interpolert posisjon eller krysningspunktet til to kurser.

I mange tilfeller er det nødvendig å skille horisontal og vertikal posisjon. Den vertikale posisjonen ønsker vi som regel å angi ved høyde eller dybde, og det som da gjenstår er å angi den horisontale posisjonen.

En velkjent mulighet er lengde- og breddegrad, men mange beregninger blir da unødvendig kompliserte. Lengdegrad er dessuten singulær (udefinert) på nord- og sydpolen, og i nærheten av polene vil vi ha uønskede egenskaper, slik som at lengdegradsberegninger avhenger sterkt av breddegrad. Vi har også en diskontinuitet ved datolinjen, hvor lengdegrad hopper mellom ±180° (noe som bl.a. har gitt problemer for jagerflyene F-22). Disse egenskapene gjør at beregninger som har tilstrekkelig nøyaktighet noen steder, kan gi altfor store feil andre steder.

For å omgå problemene med lengde- og breddegrad lager man ofte lokale løsninger, slik som f.eks. en kartprojeksjon eller et North-East-Down-system (lokale flat-jord-antagelser). Ulempene med disse er at de har begrenset geografisk gyldighet. Mange beregninger blir her bare omtrentlige og feilen øker ofte med avstand. For å håndtere større avstander brukes kompliserende tiltak som reposisjonering av tangentpunkt eller bruk av flere tilstøtende kartprojeksjoner, slik som i UTM (Universal Transverse Mercator). Gyldighet i polområdene er også en utfordring her.

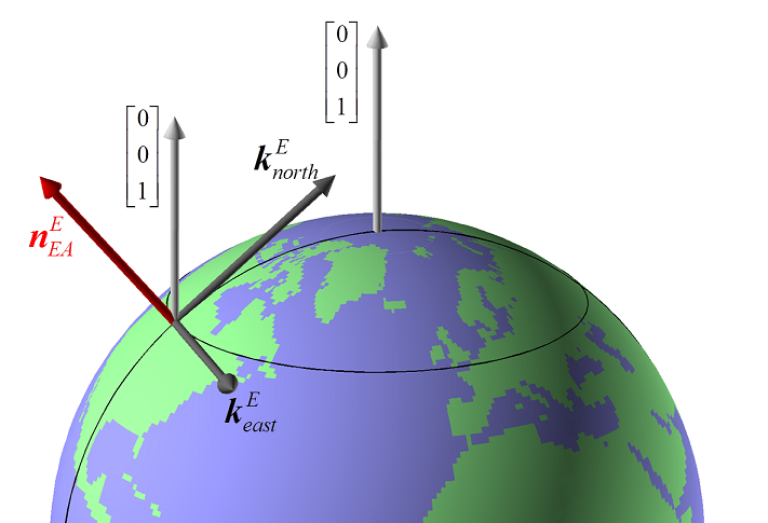
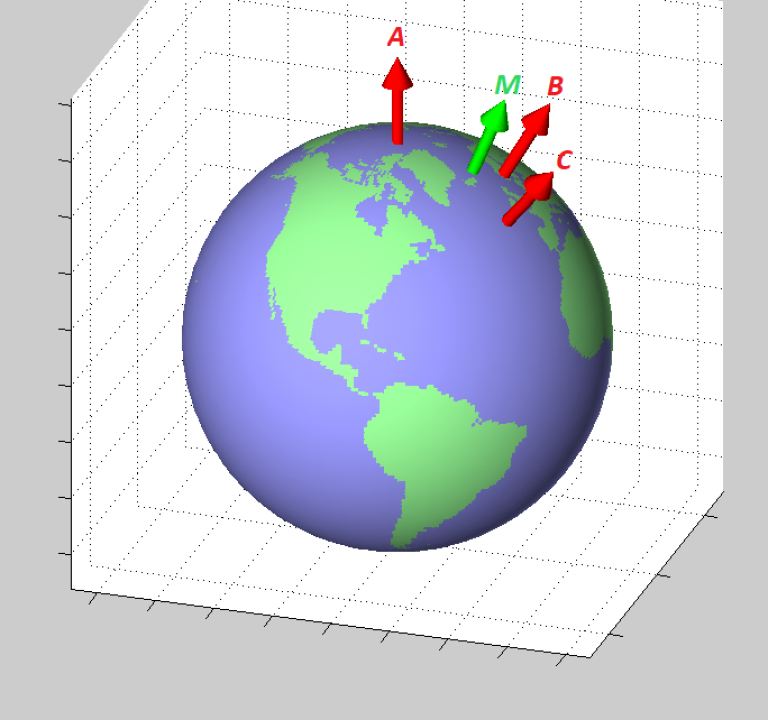
For å unngå problemene nevnt over har FFI introdusert et alternativ, som er å angi horisontal posisjon ved hjelp av normalvektoren til jordellipsoiden. Vi kaller dette alternativet n-vektor. Denne har ingen singulariteter eller diskontinuiteter, og således behandles alle steder på jorda likt. Siden dette er en 3D vektor kan man løse svært mange posisjonsberegninger med velkjent vektoralgebra, og det viser seg at løsningene ofte blir både enkle og elegante. Hvis man for eksempel skal finne ut hvor to kurser vil krysse hverandre, kreves flere sider med kode når man bruker lengde- og breddegrad, mens med n-vektor holder det med to enkle kodelinjer.

Etter at FFI presenterte n-vektor i Journal of Navigation har stadig flere utenfor FFI tatt den i bruk, og et eksempel på bruker er Thales, som er verdens største på Air Traffic Management (ATM). n-vektor og fremgangsmåtene beskrevet i artikkelen har nå erstattet andre alternativer i deres nyeste generasjon av ATM. I 2022 tok Kystverket i bruk n-vektor i overvåkningen av skipstrafikken i norske farvann, hvor en viktig hensikt er å unngå kollisjoner.